Příklad 1:

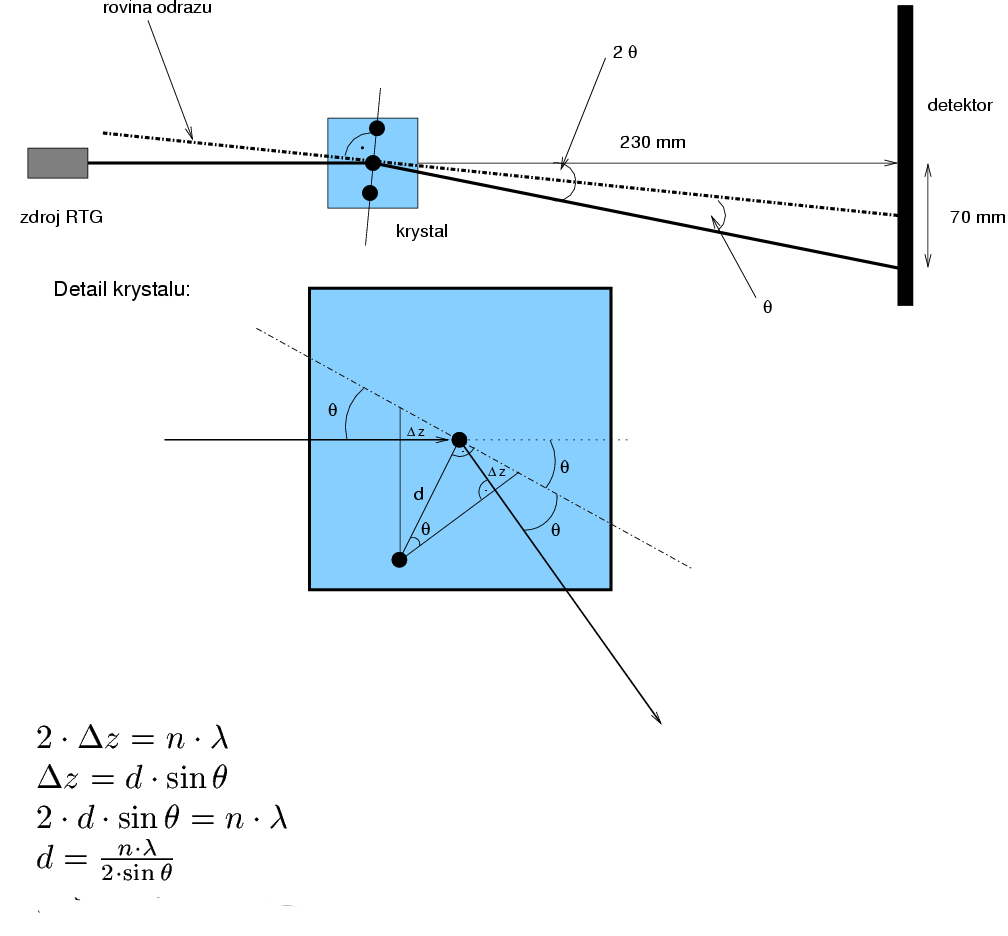
Při difrakčním experimentu byly na plošném detektoru umístěném 230 mm od krystalu zřetelné všechny difrakce až do vzdálenosti 70 mm od středu detektoru. Jaké bylo efektivní rozlišení měření, používalo-li se přitom synchrotronové záření o vlnové délce 0.95 Å?

Výsledek:

Rozlišení: 0.32 nm

Řešení:

Úhel θ vypočítáme z tg(2θ) = 70/230. Rozlišení je nejmenší vzdálenost d odpovídající n=1 a největšímu úhlu θ.

Příklad 2:

Očíslujte uvedené metody řešení fázového problému difrakčního experimentu podle pracnosti přípravy krystalu vzorku, kterým je oligodeoxyribonukleotid tvořící krátkou pravidelnou dvojšroubovici (1 - nejméně pracná). Metody pro daný vzorek nepoužitelné označte nulou.

• chemická styntéza s použitím bromuracilu a měření při různých λ
• molekulové přemístnění
• příprava krystalu nativní molekuly a dvou krystalů s různými těžkými kovy, měření při jedné vlnové délce
• molekulárně genetické zavedení selenomethioninu a měření při různých λ
• příprava krystalu s těžkým kovem a bez těžkého kovu, měření anomálního rozptylu při jedné vlnové délce

Výsledky:

• 2
• 1
• lze uznat 0 nebo 4
• 0
• lze uznat 0 nebo 3

Příklad 3:

Na základě schematického nákresu rozmístění těžkých atomů v dvojrozměrněrné elementární buňce nakreslete čtyři buňky odpovídající Pattersonovy mapy (dvě nad sebou a dvě vedle sebe).

Výsledek:

Řešení:

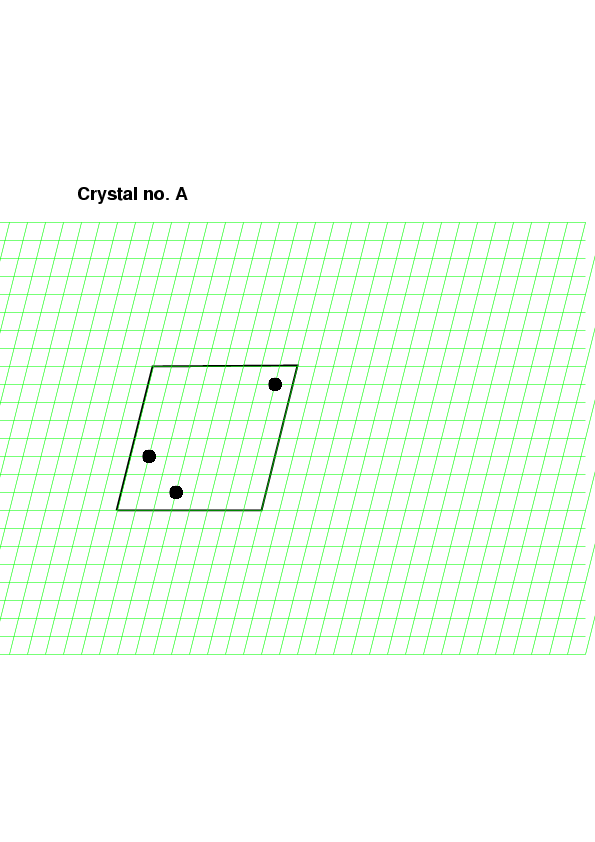
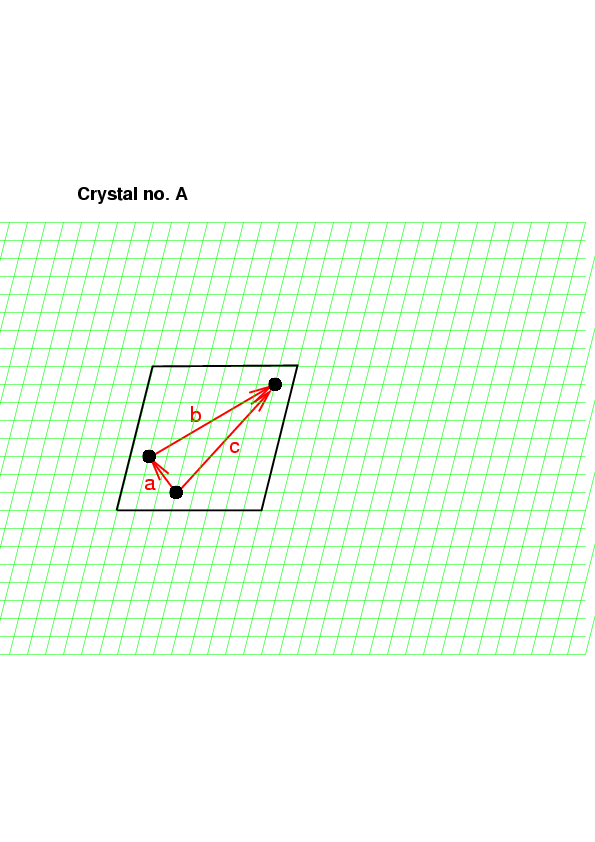
Nejprve určíme všechny meziatomové vektory (na následujícím obrázku jsou tři nakresleny červeně, další tři jsou orientovány opačně)

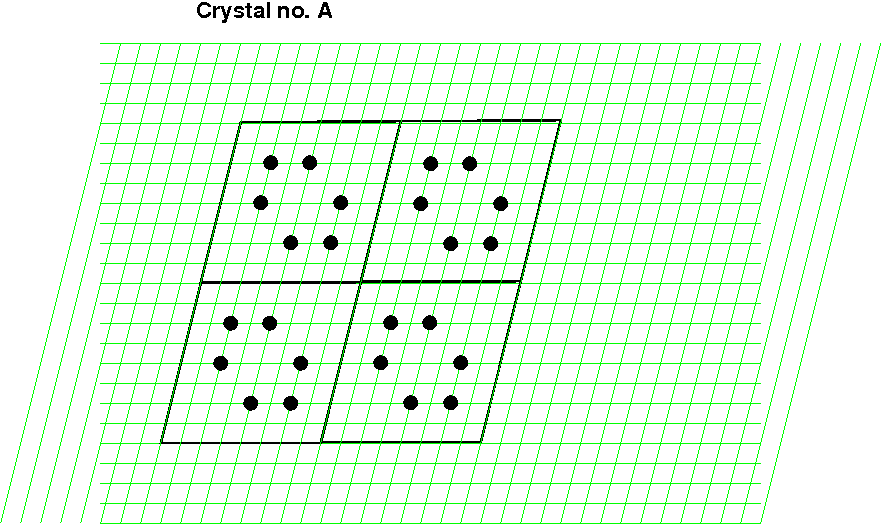
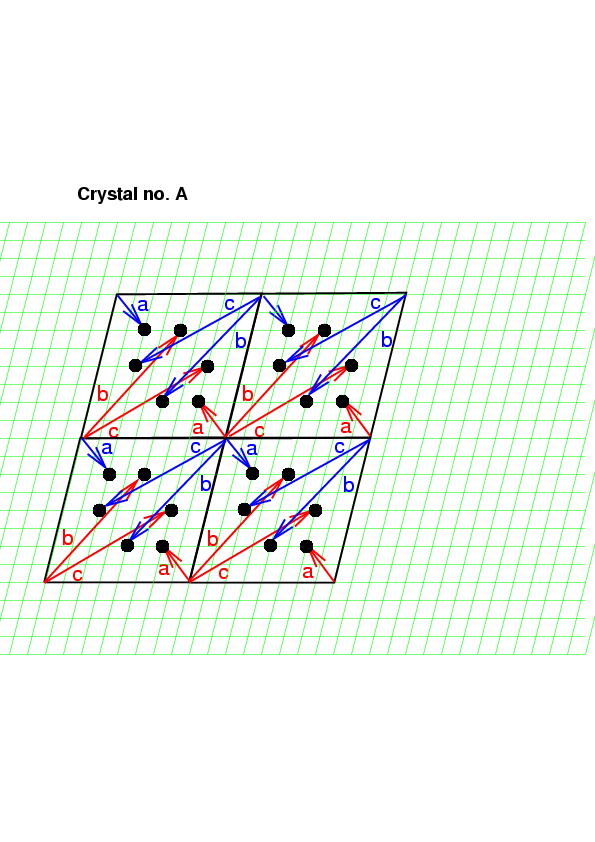
Do každého rohu čtyř buněk mřížky (stejně velkých jako v zadání) umístíme počátky všech šesti meziatomových vektorů (vektory nakreslené v předchozím obrázku jsou v následujícím obrázku nakresleny červeně, opačné vektory modře). Do koncových bodů všech vektorů, které směřují dovnitř našich čtyř buněk, zakreslíme body Pattersonovy mapy.

Příklad 4:

Jak se sníží počet stupňů volnosti volné aminokyseliny tyrosinu, popíšeme-li její vedlejší řetězec jako tuhé těleso? (uvažujte pouze těžké atomy)

Výsledek:

V případě těžkých atomů se sníží počet stupňů volnosti z 39 na 17.

Řešení:

Volný tyrosin má 13 těžkých atomů (N=13), tedy 39 (3N) stupňů volnosti. Z toho postranní řetězec je tvořen osmi těžkými atomy, jejich poloha je v přiblížení tuhého tělesa dána dvěma torzními úhly. Proto přechod k tuhému tělesu znamená náhradu 3.8=24 stupňů volnosti dvěma (=torzní úhly). Celkový počet stupňů volnosti se proto sníží o 22 (z 39 na 17).